Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change sizeLet's start from a picture that represents our reflection vector and the other vectors used in the calculation A representation of theGeometry Transformations If there is one prayer that you should pray/sing every day and every hour, it is the LORD's prayer (Our FATHER in Heaven prayer) It is the most powerful prayer A pure heart, a clean mind, and a clear conscience is necessary for it Samuel Dominic Chukwuemeka O LORD my GOD, please bless me always with 1 Samuel 226

What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic
Reflection over y=x calculator
Reflection over y=x calculator-Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)
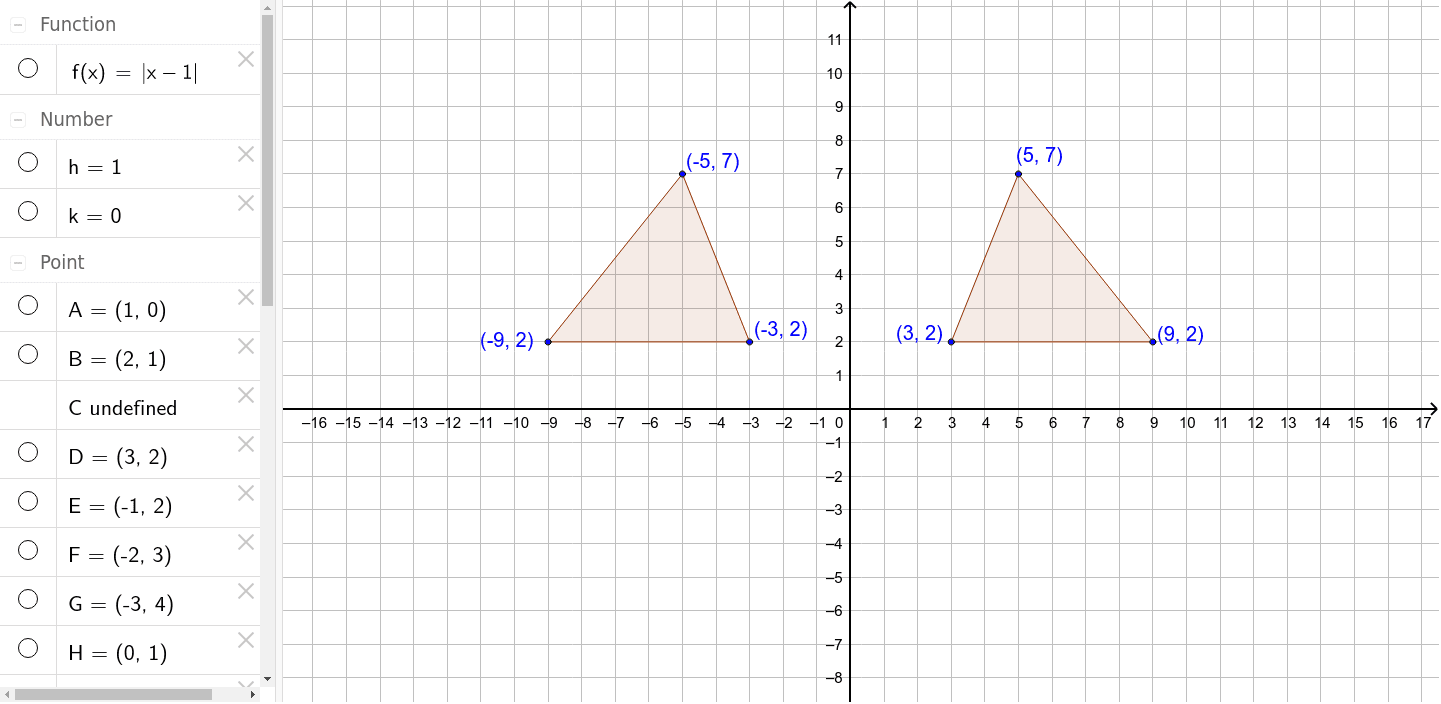



Reflection Over The Y Axis Geogebra
The reflection formula produces $\left(\frac{41}{13},\frac3{13}\right)$, which you can verify is perpendicular to the vector $\mathbf r$ computed previously The equation of the outgoing line is then $41x3y=\dots$ (I've multiplied the entire equation byFor example, when reflecting the point (2,5) over y=x it becomes (5,2) This is very simple, but why does it work?Geometry reflection A reflection is a "flip" of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection
A reflection of a point over the y axis is shown The rule for a reflection over the y axis is (x, y) → (− x, y) Reflection in the line y = x A reflection of a point over the line y = x is shownA reflection is a flip over a line You can try reflecting some shapes about different mirror lines here How Do I Do It Myself?Just approach it stepbystep For each corner of the shape 1 Measure from the point to the mirror line (must hit the mirror line at a right angle) 2
Calculus Integral with adjustable bounds example Calculus Fundamental Theorem of CalculusIf (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed; Amazing FREE first reflection points calculator software for setting your room, by Andreas Melcher Andreas Melcher was kind enough to show me his application It´s a great online tool where you can calculate all reflections in a room Paint dimensions of your room, place speaker and listening position, this app will show ray tracing of the room




Reflection Over The Y Axis Geogebra




How To Find A Reflection Image
The resulting orientation of the two figures are oppositeReflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflectionReflect over XAxis Example How to reflect over the xaxis?
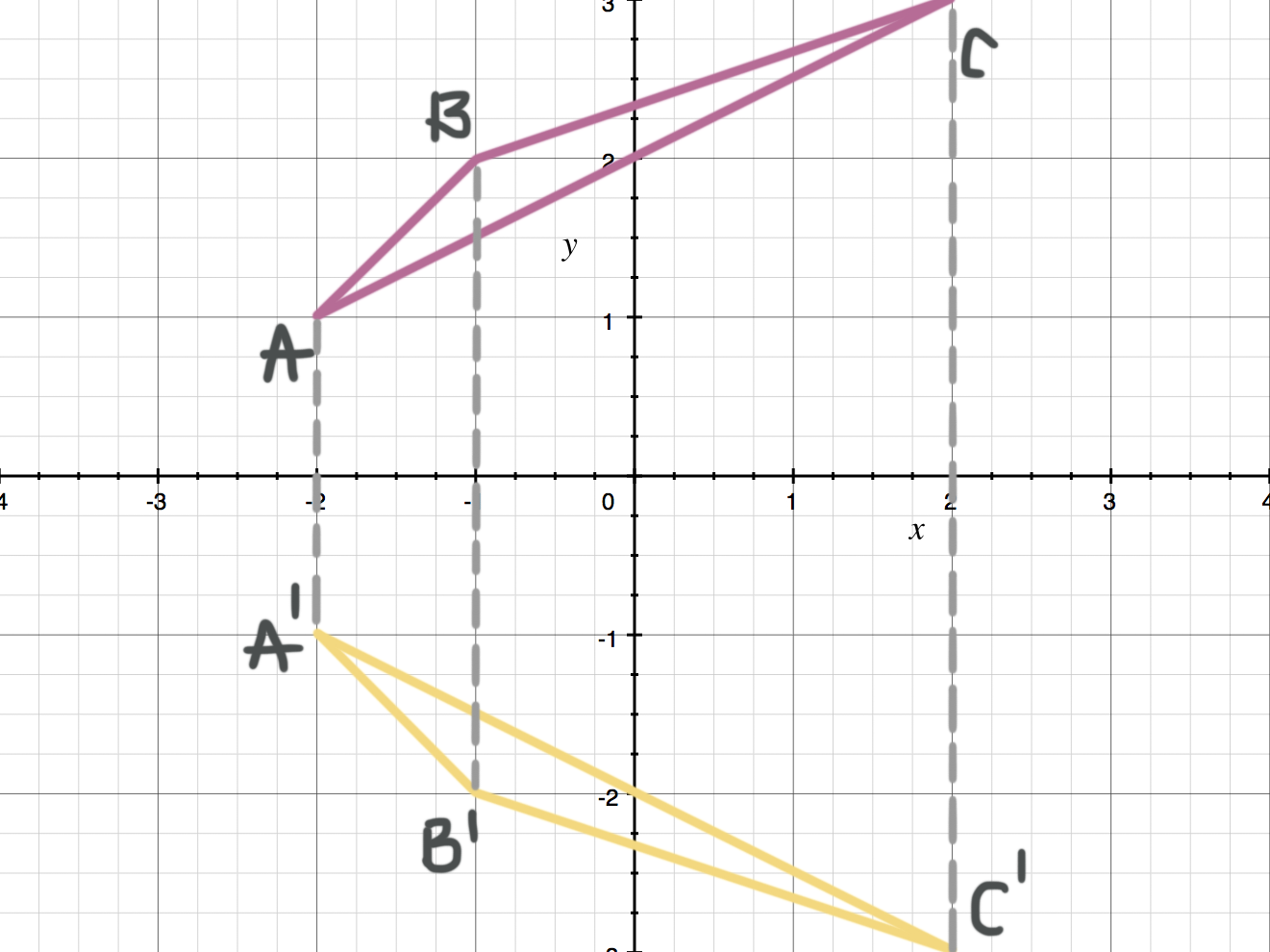



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Linear Algebra Reflection In Any Linear Line Y Ax B Youtube
Reflection line points ShareThe following formula can be used to calculate the coordinate point in the xy plane that has rotated by some angle (θ) about the xaxis Note these formulas are for clockwise rotation X=xcos (θ)ysin (θ) Y=−xsin (θ)ycos (θ) Where X is the new X coordinate Y is the new Y coordinate and θ is the angle of rotationA point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxis For a point reflection, we actually reflect over a specific point, usually that point is the origin Formula r (o r i g i n) (a, b) → (− a, − b)




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Transformation Matrix
Math geometry 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflect over x= 1 reflection over the line y=x Reflection over y=x reflection over yaxisSWBAT reflect an image over y=xPractice2 Alex Phipps Ch6 Geogebra Project Systems of Linear Equations Find the distance between the point and line (without vectors) Modeling a Pair of (Hollow) Slippers in GeoGebra Augmented Reality
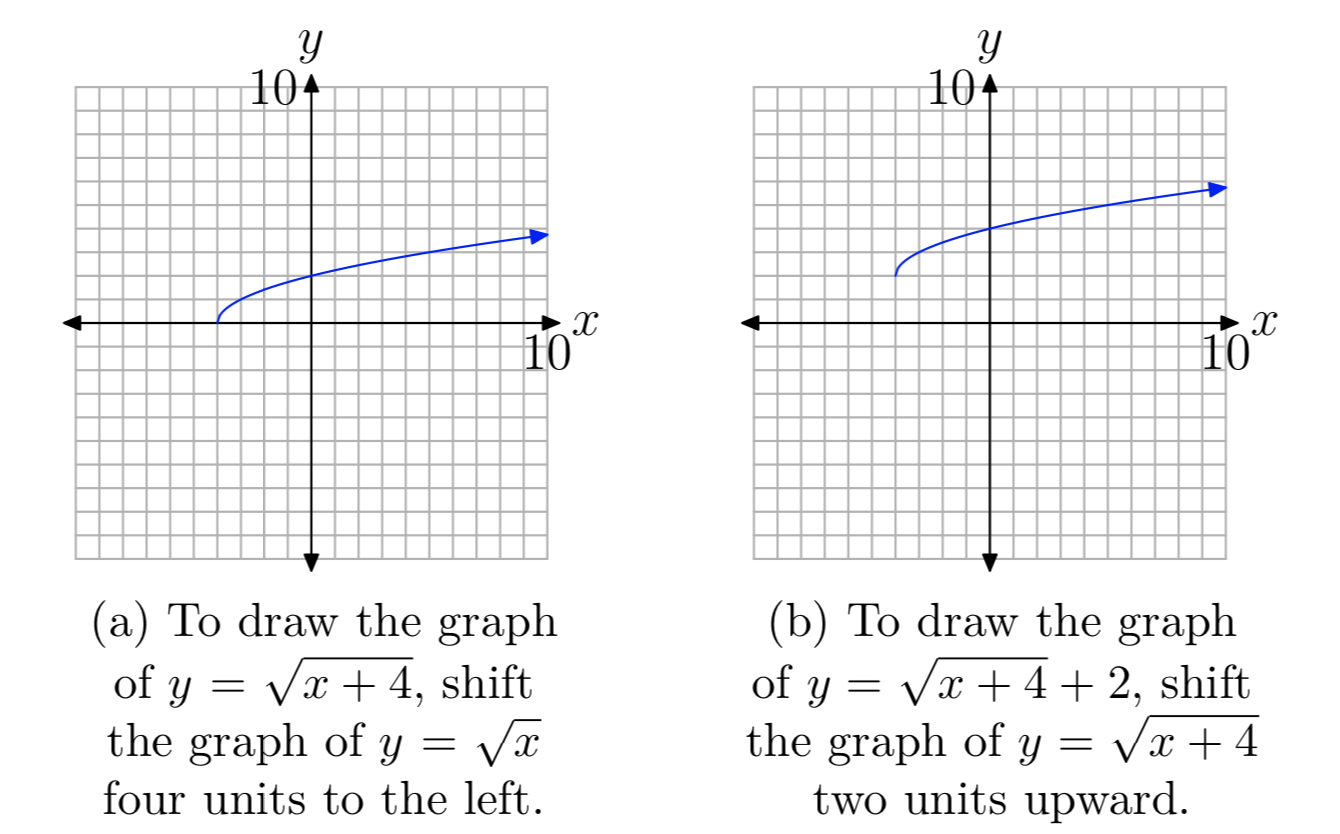



9 1 The Square Root Function Mathematics Libretexts



2
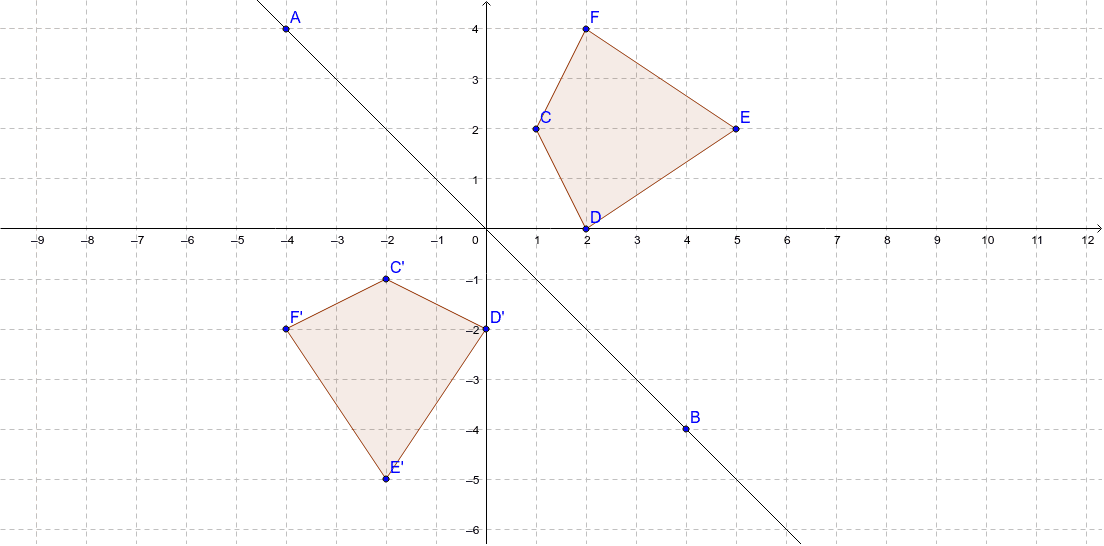
First, determine the original coordinate points For this example, we will say the coordinate points are (4,5) Next, calculate the new coordinate points Using the formula above we calculate the new reflected points asThe line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I wiThe line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 When reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x




Reflection Rules How To W 25 Step By Step Examples




Orthocenter Calculator Definition Formula
Problem 1 Find a linear transformation rule of the form (p, q) → (r, s) such that the reflection image of the point (p, q) over the oblique line y = mx b is the point (r, s) In the general case, both r and s are functions of p, q, m and bFirst you have to get the perpendicular s(x) = ms ⋅x t s ( x) = m s ⋅ x t (the dashed red line) You have to know this ms = − 1 m m s = − 1 m And then you know that P P is on s s So you simply put in the values x,y x, y of P and solve to t t t = y−ms ⋅x t = y − m s ⋅ x Now you have s s As s s and g g have exactly pointGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha
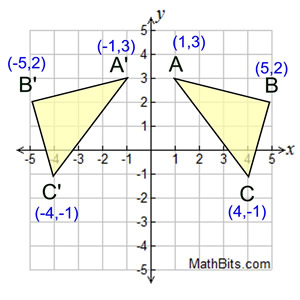



Reflection Mathbitsnotebook Geo Ccss Math
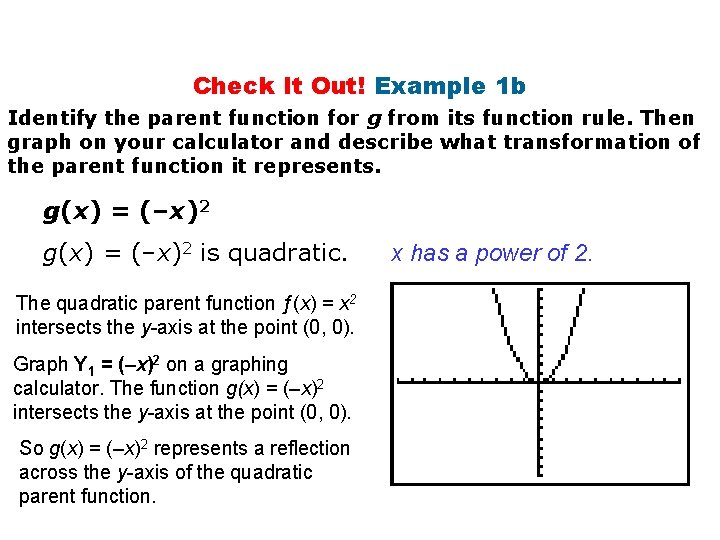



1 9 Introduction To Parent Functions Holt Algebra
Reflection, Geometric Transformations Click and drag the blue dot to see it's reflection across the line y=x (the green dot) Pay attention to the coordinates How are they related to each other?Functions & Graphing Calculator \square!I was trying to understand how to calculate the reflection vector and found these answers I couldn't understand them easily, so I took my time to do it myself, the good thing is that I can now detail it in an ELI5 fashion!



View Question Let P 5 1 And Let Q Be The Reflection Of P Over The Line Y 1 2x 2 Find The Coordinates Of Q




The Graph Of F X Startroot X Endroot Is Reflected Over The Y Axis Use The Graphing Calculator To Brainly Com
How do you prove that the point P (x,y) becomes P' (y,x) after reflecting upon the line y=x? 4 Reflection along with the line In this kind of Reflection, the value of X is equal to the value of Y We can represent the Reflection along yaxis by following equation Y=X, then the points are (Y, X) Y= – X, then the points are ( – Y, – X) We can also represent Reflection in the form of matrix – Homogeneous CoordinateStart your free trial In partnership with
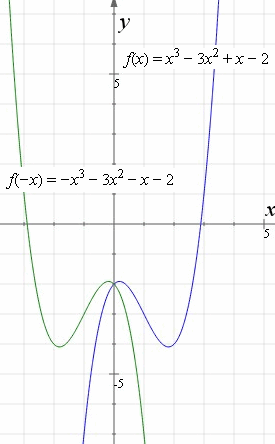



How To Reflect A Graph Through The X Axis Y Axis Or Origin
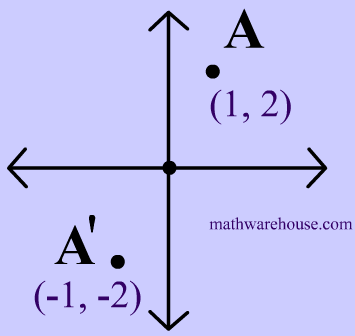



Point Reflections Formula And Examples Explained With Applet Examples And Practice Problems Center At Origin And At Any Arbitrary Point
Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Reflection Over the XAxis For our first example let's stick to the very simple parent graph of y = x^2 {See video for graph} On the screen you can see that the graph of this equation is a parabola From the diagram we see the object point ( − 2, −5) is mapped to (x',y') by a reflection in the line X = 2 we note (1) the ycoordinate is unaffected (2) for reflections the distance from the line of reflection to the object is equal to the distance to the image point ∴ a = 2 2 = 4units so the image point is 4 units from the line of
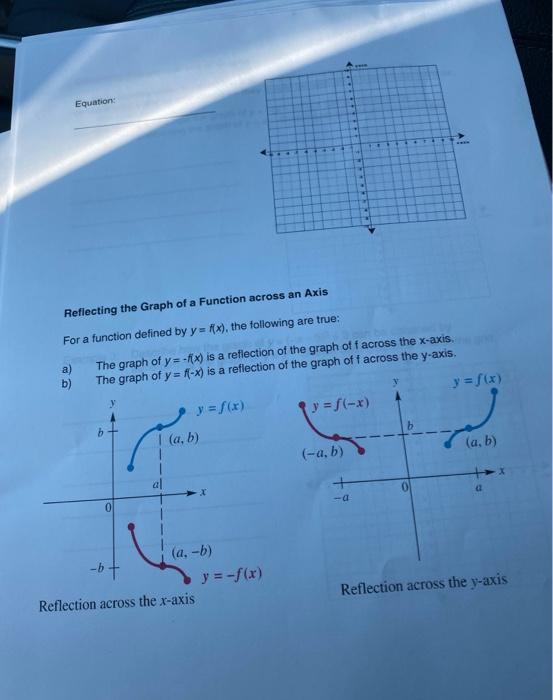



Solved Name Section 2 3 Reflecting Graphs Reflecting Acr Chegg Com




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
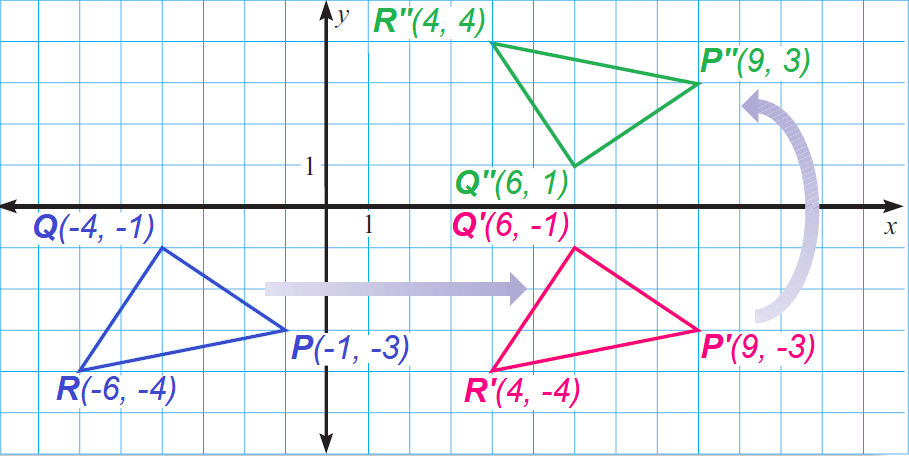
Glide Reflection A glide reflection is a composition of transformations In a glide reflection, a translation is first performed on the figure, then it is reflected over a line Therefore, the only required information is the translation rule and a line to reflect over A common example of glide reflections is footsteps in the sand Therefore, the reflection of the point (x, y) across Xaxis is (x, y) Reflection over Yaxis When a point is reflected across the Yaxis, the Ycoordinates remain the same But the Xcoordinates are transformed into its opposite signs Therefore, the reflection of the point (x, y) across Yaxis is (x, y) Reflection over Y = XThe above point reflection calculator is capable of giving point reflection for your coordinates based on the Xaxis, Yaxis, and origin Feel free to try this point reflection calculator to




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Reflection Over The Y X Line Youtube
Suppose Tis the transformation from R2 to R2 that results from a reflection over the line yx followed by a y compression by 1/4 Find the matrix A that induces T Get more help from Chegg Solve it with our algebra problem solver and calculator(Turn on #3 and #4 below to begin exploring this) The formula to calculate the reflection direction is R = 2 ( N ^ ⋅ L ^) N ^ − L ^ R = 2 ( {\hat {N}}\cdot {\hat {L}}) {\hat {N}} {\hat {L}} R = 2(N ^ ⋅L^)N ^ −L^ How is this formula obtained?
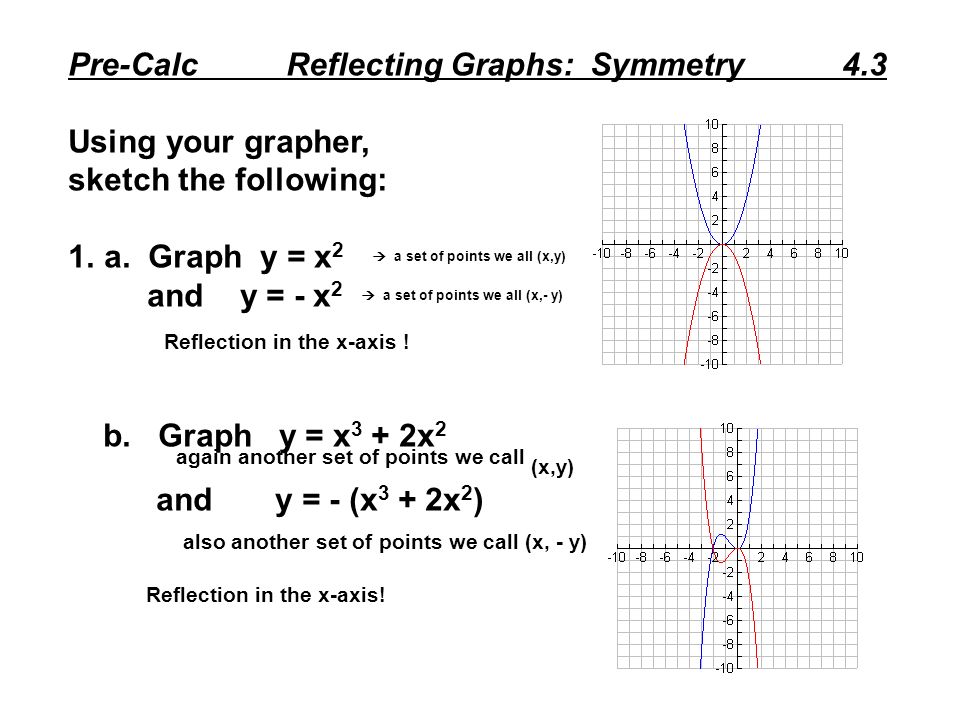



Pre Calc Reflecting Graphs Symmetry 4 3 Using Your Grapher Sketch The Following 1 A Graph Y X 2 A Set Of Points We All X Y And Y X 2 A Ppt Download




Reflection Transformation Matrix
Basic Math Math Calculator Step 1 Enter the expression you want to evaluate The Math Calculator will evaluate your problem down to a final solution You can also add, subtraction, multiply, and divide and complete any arithmetic you need Step 2 Click the blue arrow to submit and see your result!Free graphing calculator instantly graphs your math problemsThe linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (m



Reflections Of A Graph Topics In Precalculus
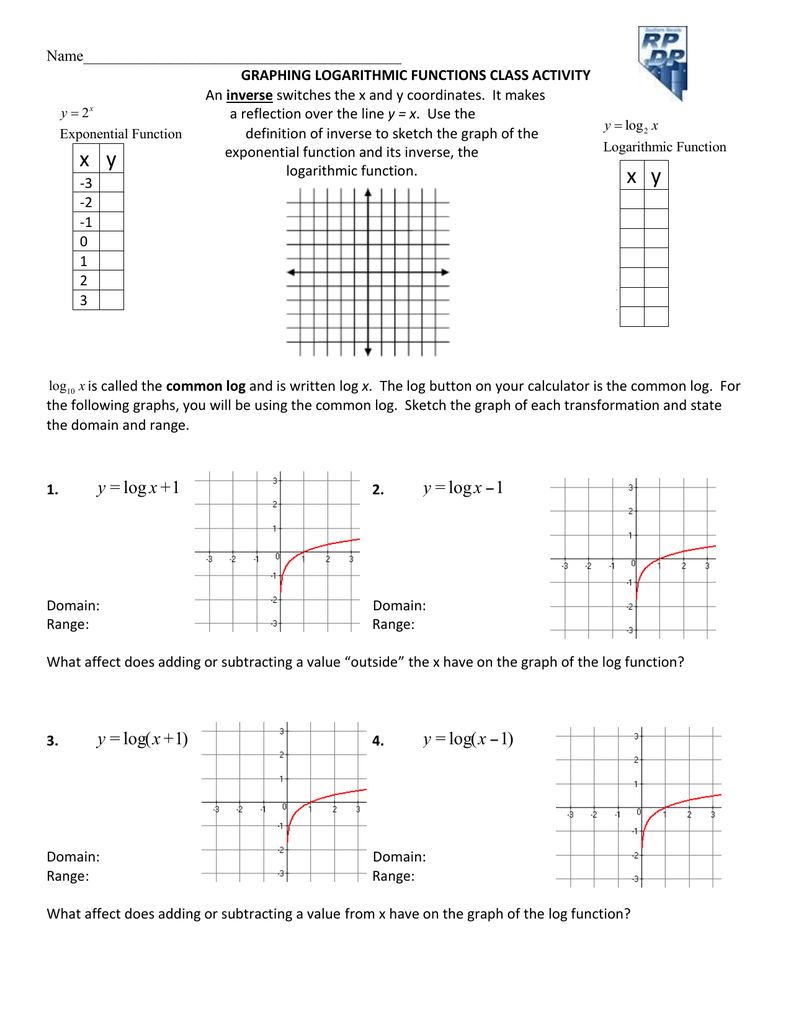



Name Inverse Y X
Viewed 3k times 1 I have been looking at how to reflect a point in a line, and found this question which seems to do the trick, giving this formula to calculate the reflected point Given (x,y) and a line y = ax c we want the point (x', y') reflected on the line Set d= (x (y c)*a)/ (1 a^2) Then x' = 2*d x and y' = 2*d*a y 2cReflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABCGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Transformation Reflection Over X Axis
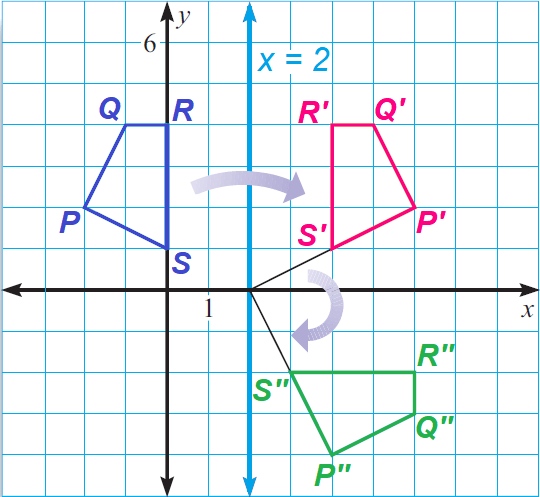



Glide Reflections And Compositions
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflection When a figure is reflected across the yaxis, as shown below, the xvalues become opposites while the yvalues remain the same The notation or
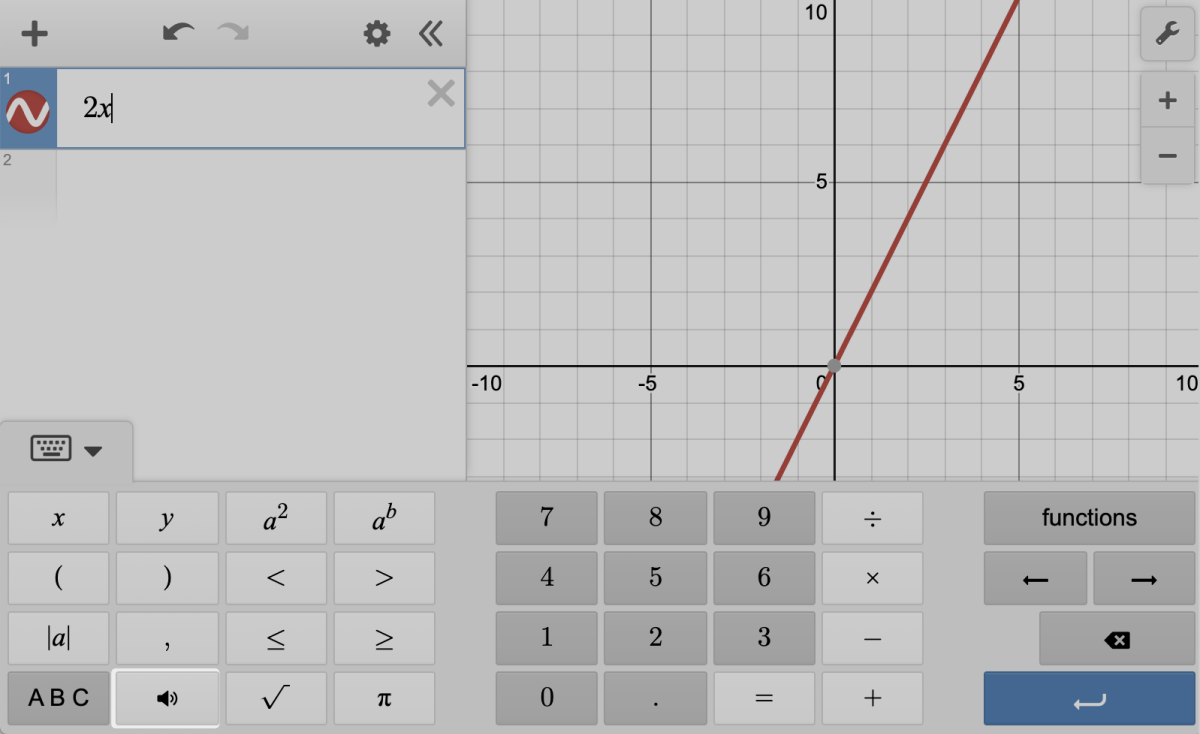



Desmos Accessibility




21 T Math Geo T1 Cbt Section 1 No Calculator Section Question 1 4 Based On The Graph Brainly Com
Inverse Trigonometric Functions are used to find angles Graphically, inverse functions are reflections over the line y = x Take the graph of y = sin x in Figure 2a, then reflect it over y = x to form the inverse as in Figure 2b Notice the inverse fails the vertical line test and thus is not aI did develop the formula using the 3 steps shown in the graphic I describe them bellowReflection around y=x Log InorSign Up Here is an example of another kind of reflection that will frequently arise in our discussion of functions 1 What happens when we replace our xvalue with our yvalue and our yvalue with our xvalue?
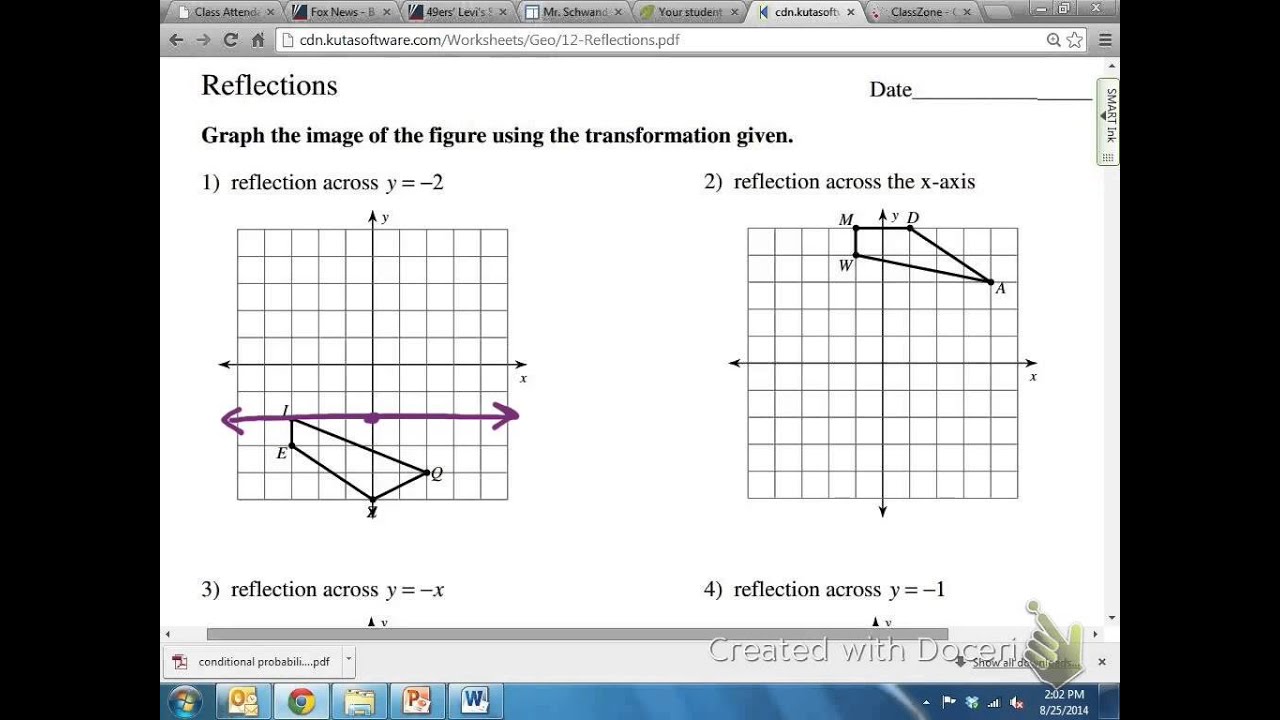



Common Core Math Geometric Reflection Over Y 2 Youtube



Reflect Over X Axis Calculator Calculator Academy
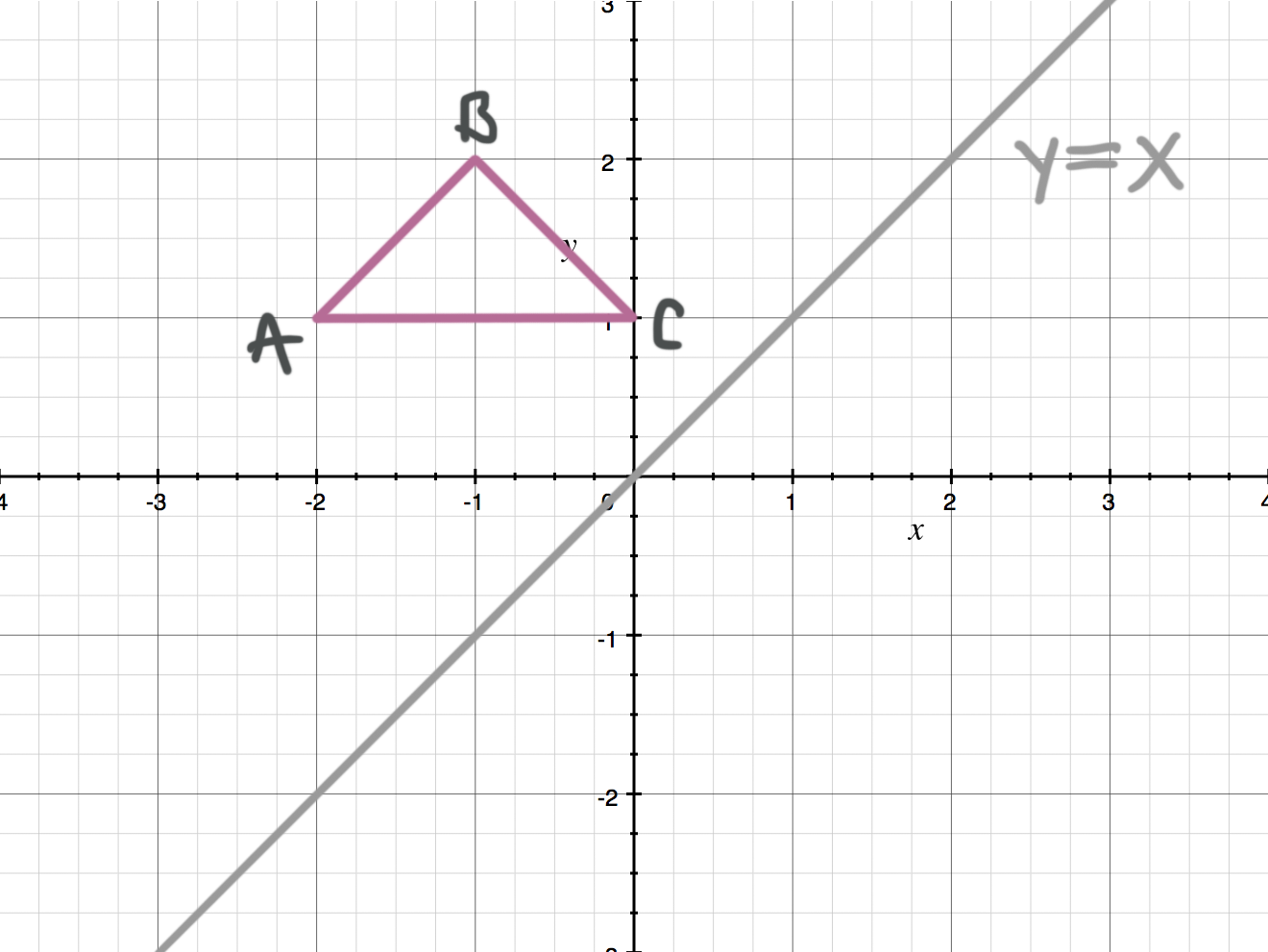



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Polar Coordinates Equations And Graphs She Loves Math
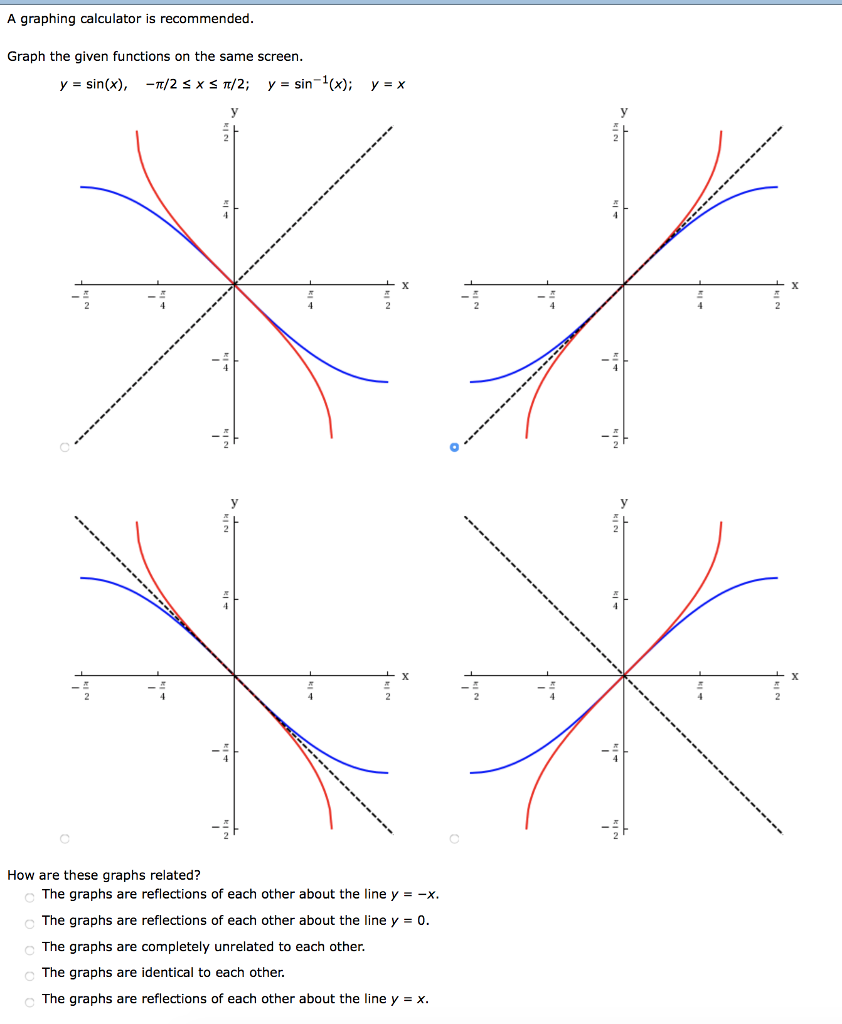



A Graphing Calculator Is Recommended Graph The Chegg Com




Solved Reflecting Across The Y Axis To Set Up This Activi Chegg Com




Pre Calc Reflecting Graphs Symmetry 4 3 Using Your Grapher Sketch The Following 1 A Graph Y X 2 A Set Of Points We All X Y And Y X 2 A Ppt Download




Polar Coordinates Equations And Graphs She Loves Math
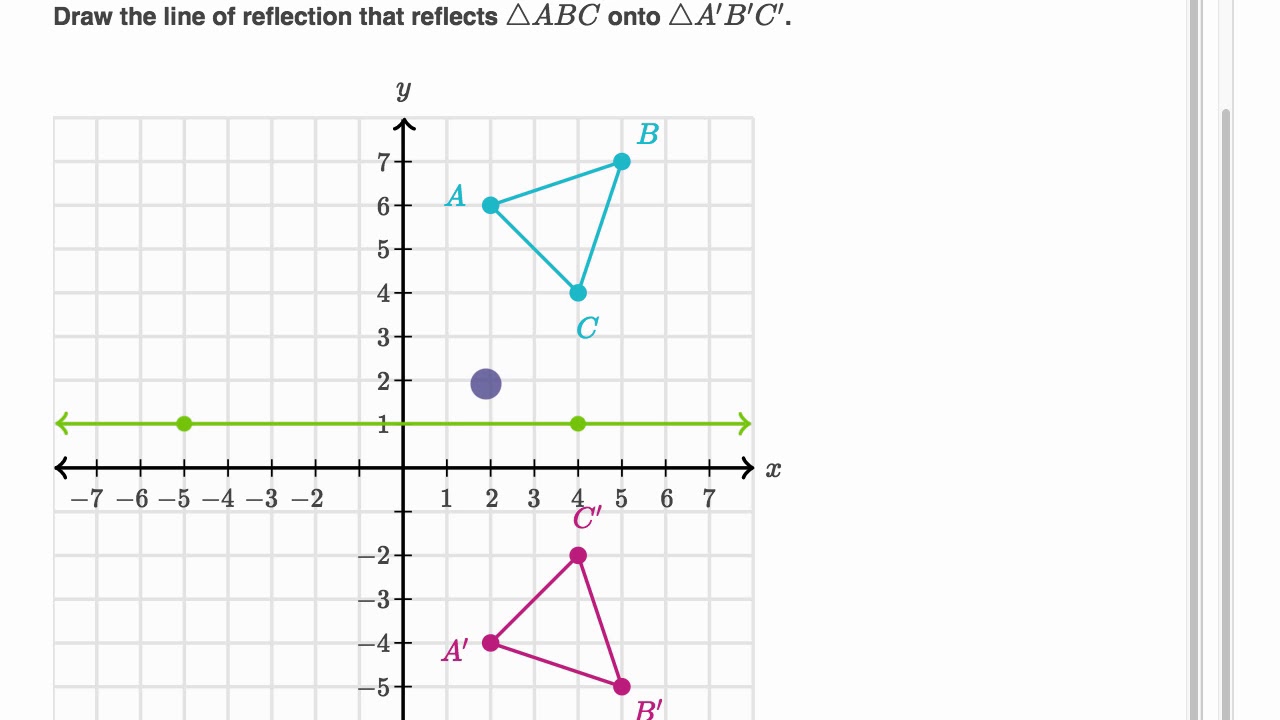



Line Of Reflection Example Youtube



R E F L E C T I O N O V E R Y X Zonealarm Results



The Adventures Of Mr Newman In Math 13




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic
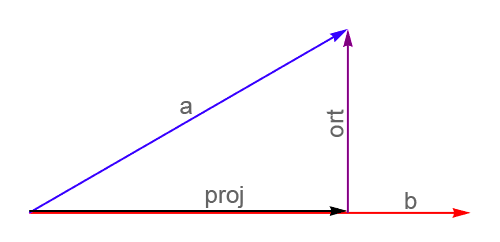



Vector Projection Calculator
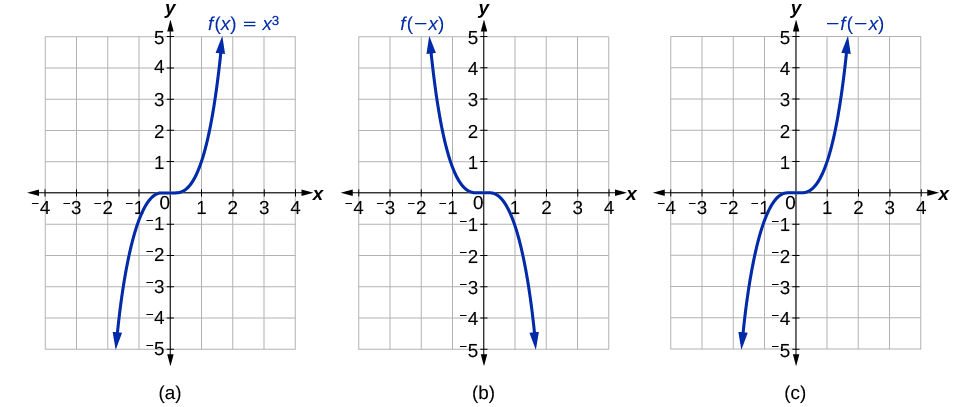



Transformation Of Functions Algebra And Trigonometry



Desmos Accessibility
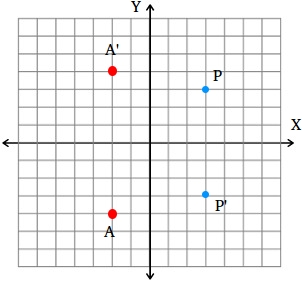



How To Find A Reflection Image




Tatukgis Coordinate Calculator
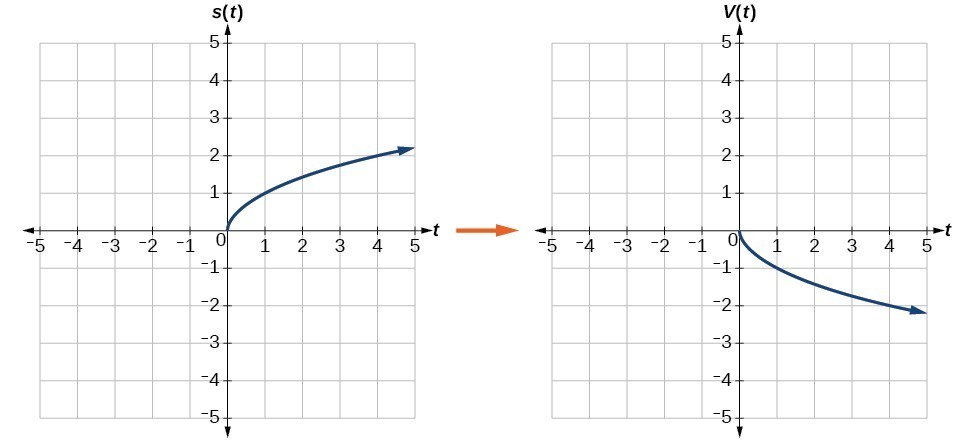



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




How To Find A Reflection Image
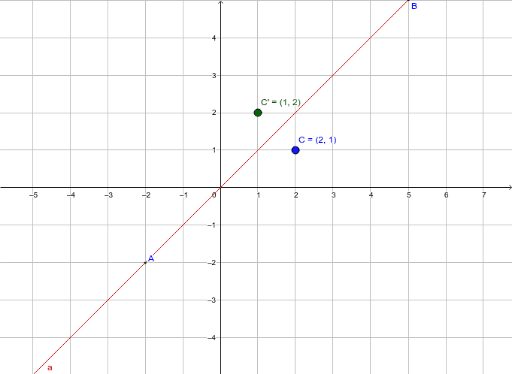



Reflection Across Y X Geogebra




Drawing The Inverse Function On The Ti 84 Graphing Calculator Inverse Functions Graphing Calculator Graphing Calculators



Hat04 03



1




Reflection Of Functions Over The X Axis And Over The Y Axis Poyser Mp4 Youtube




Identifying Vertical Stretch Or Shrink




Solved Consider The Function F X This Is A One To O Chegg Com




Reflection Rules How To W 25 Step By Step Examples



R E F L E C T I O N O V E R Y X Zonealarm Results



1




Reflection Transformation Matrix




Graphing Cubed Root Functions Ck 12 Foundation



2



Transformation Of Functions Algebra And Trigonometry



2




Reflect Over X Axis Calculator Calculator Academy




Reflection Rules How To W 25 Step By Step Examples




Act Math Practice Question 11 Answer And Explanation Crackact Com
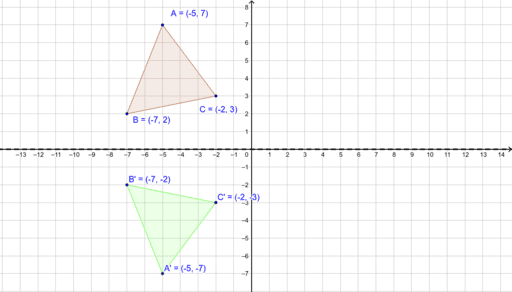



Reflection Over X Axis Geogebra




Transformation Reflection Over The Line Y X Youtube




Reflecting Functions Introduction Video Khan Academy



Reflection Over Y X Geogebra




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
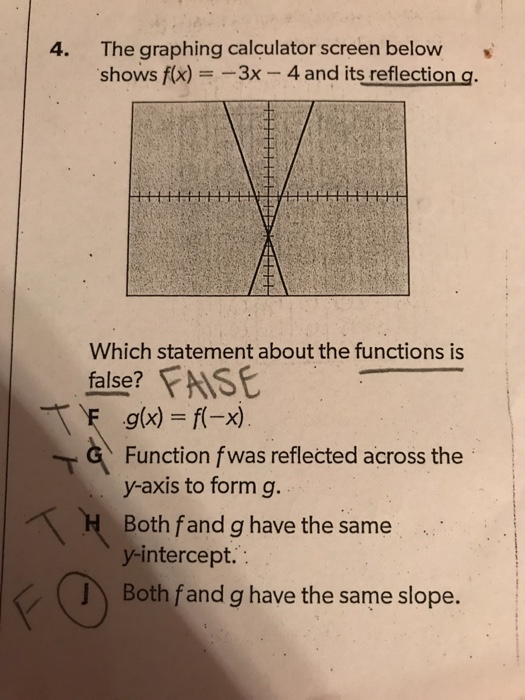



The Graphing Calculator Screen Below Shows F X Chegg Com



R E F L E C T I O N O V E R Y X Zonealarm Results



1




Reflection Over Y X Math Geometry Showme




Please Graph The Polygon And Its Image After A Reflection In The Line Y 3 What Are The Coordinates Brainly Com




Reflections




Solved Part 1 You May Not Use Your Calculator For This P Chegg Com
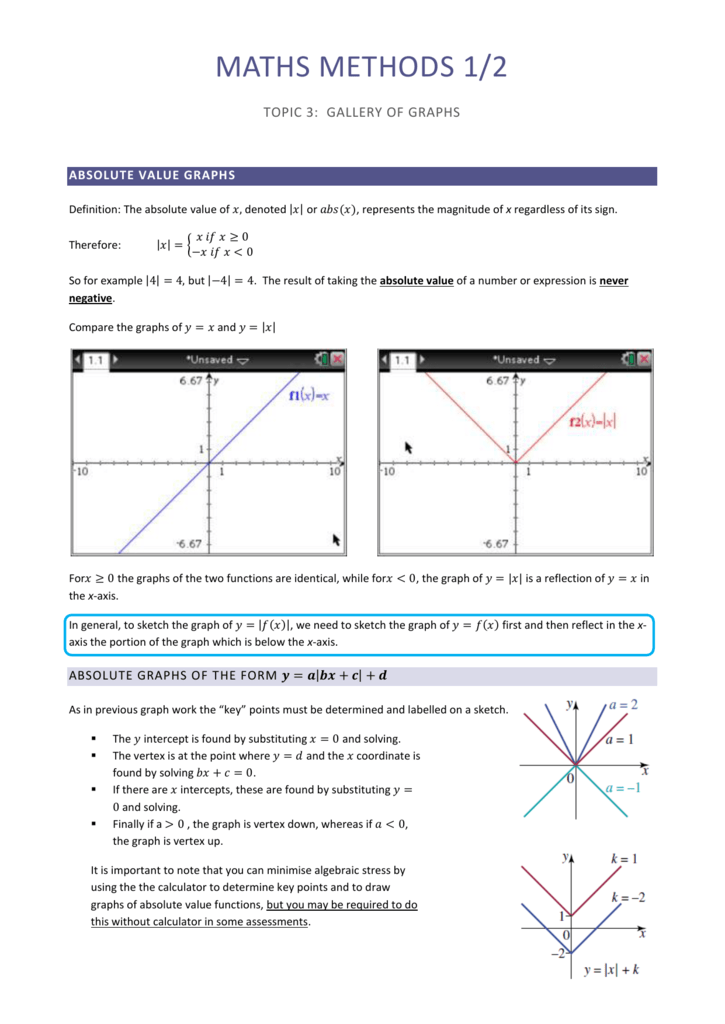



Galley Of Graphs




Scaling Reflecting Parabolas Video Khan Academy



1
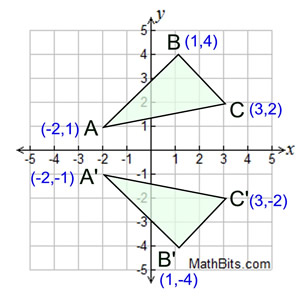



Reflection Mathbitsnotebook Geo Ccss Math
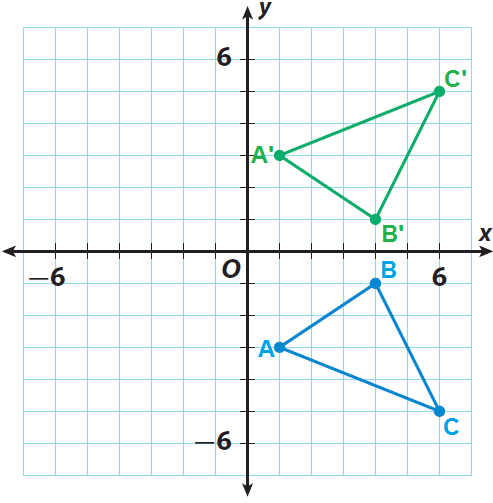



Algebraic Representations Of Reflections
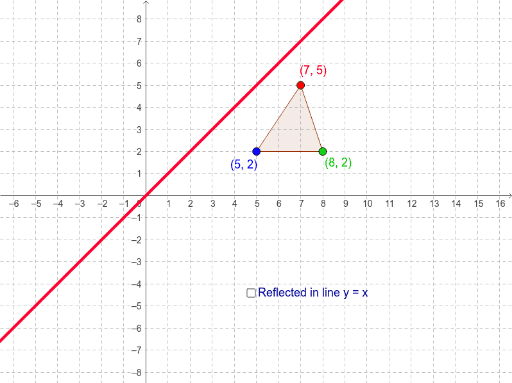



Reflection In The Line Y X Geogebra
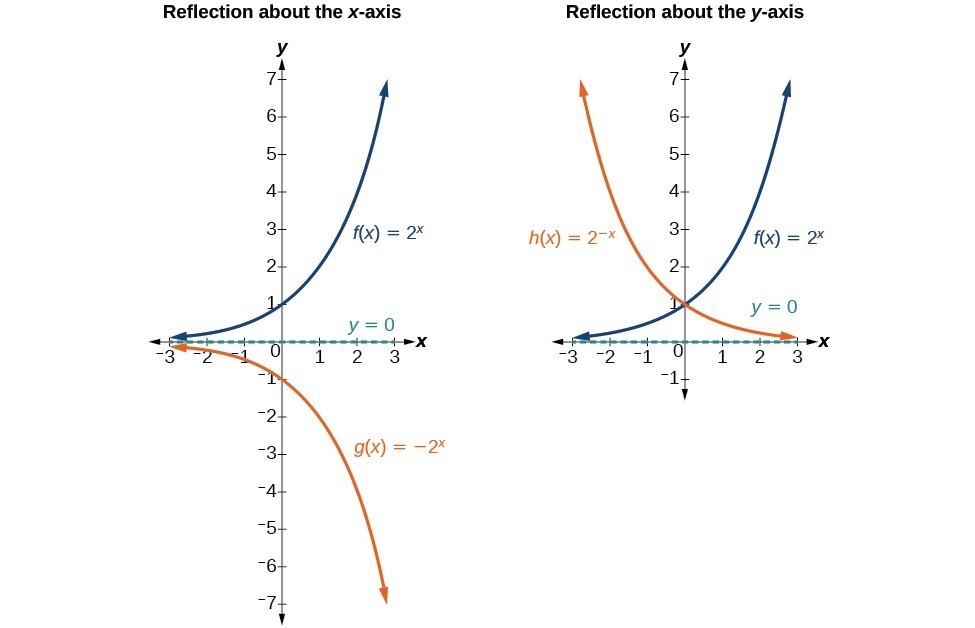



Graph Exponential Functions Using Transformations Math 1314 College Algebra
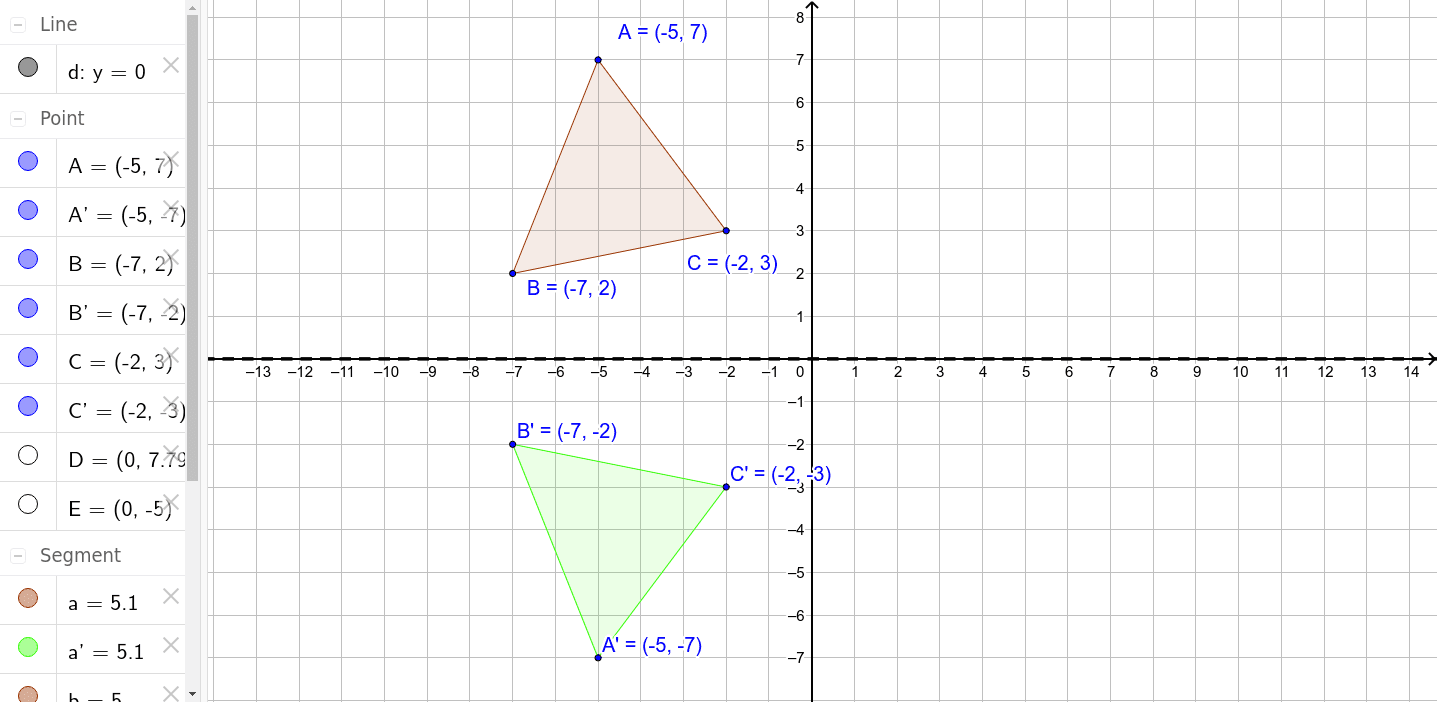



Reflection Over X Axis Geogebra



Angles Of Reflection And Refraction Calculator
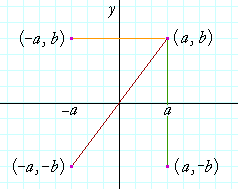



Reflections Of A Graph Topics In Precalculus
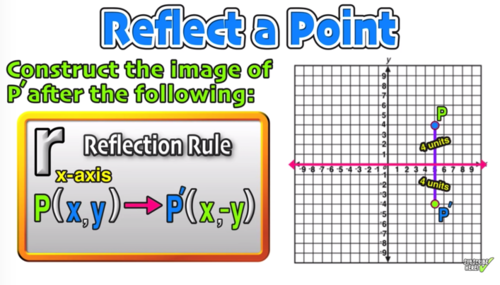



Reflection Over The X And Y Axis The Complete Guide Mashup Math
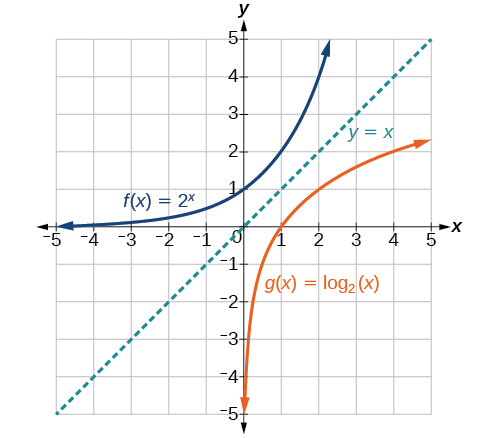



Graphs Of Logarithmic Functions College Algebra



Geometry Vivien Doucette S Digital Portfolio



Transformation Reflection Over X Axis




Percentage Calculator X Of Y Media Pandit




Transformation Of Functions Pre Calc Trig Honors Flashcards Quizlet
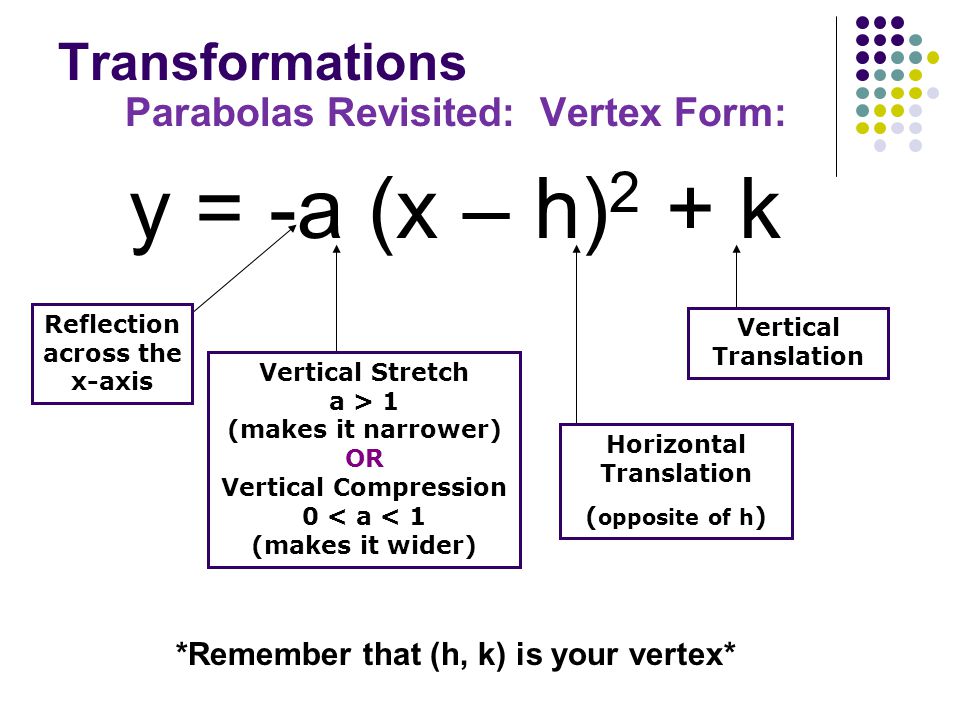



Warm Up You Should Be Able To Answer The Following Without The Use Of A Calculator 2 Graph The Following Function And State The Domain Range And Axis Ppt Download



Glide Reflections And Compositions




Reflection Transformation Matrix




Learn About Reflection Over The Line Y X Caddell Prep Online




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
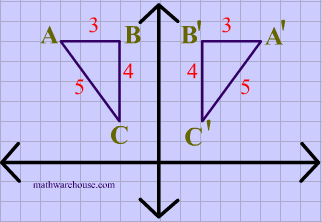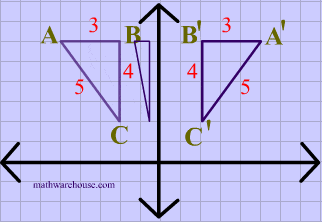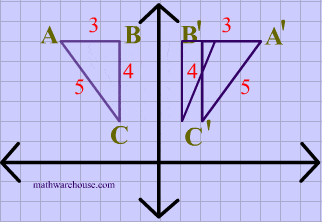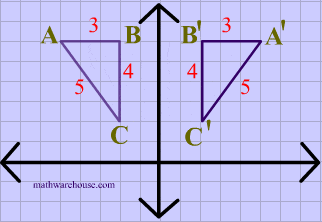



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
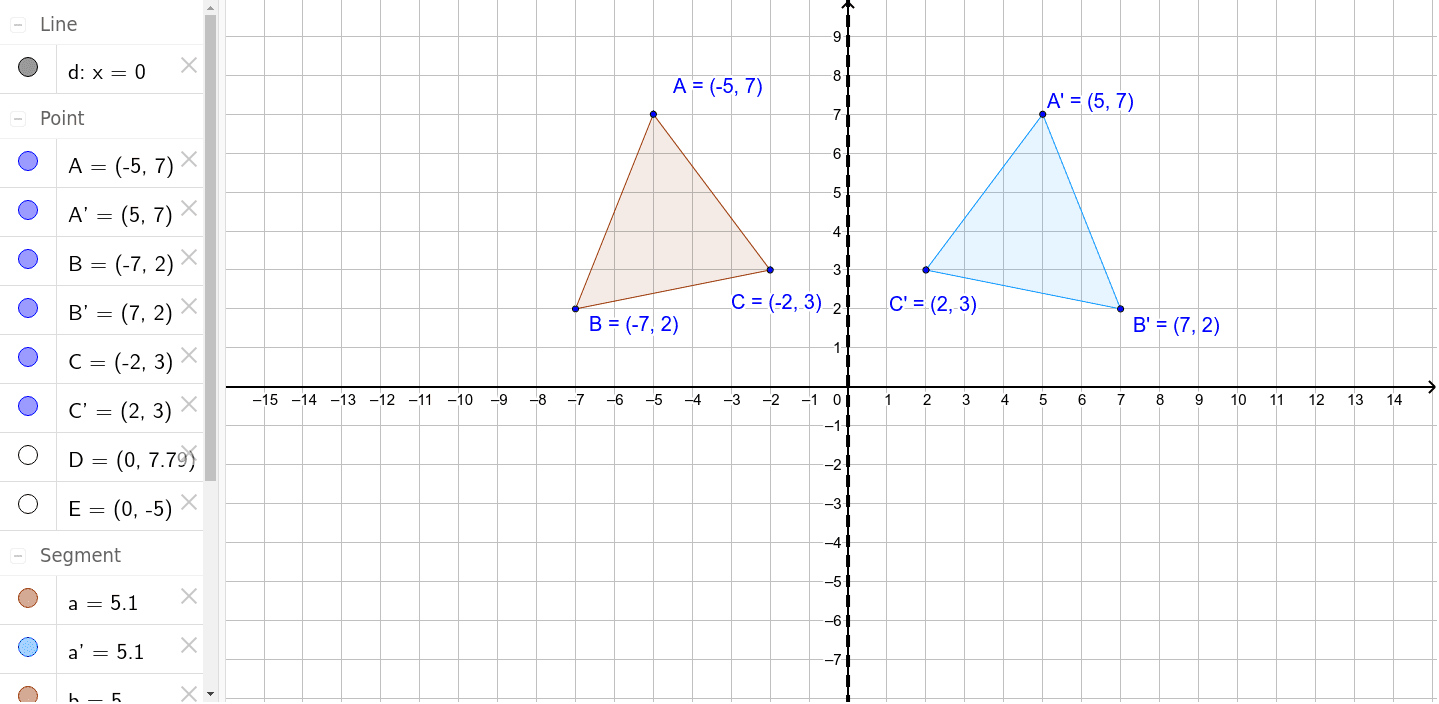



Reflection Over Y Axis Geogebra
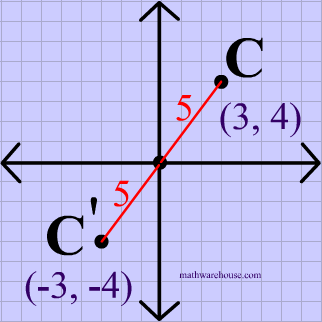



Point Reflections Formula And Examples Explained With Applet Examples And Practice Problems Center At Origin And At Any Arbitrary Point
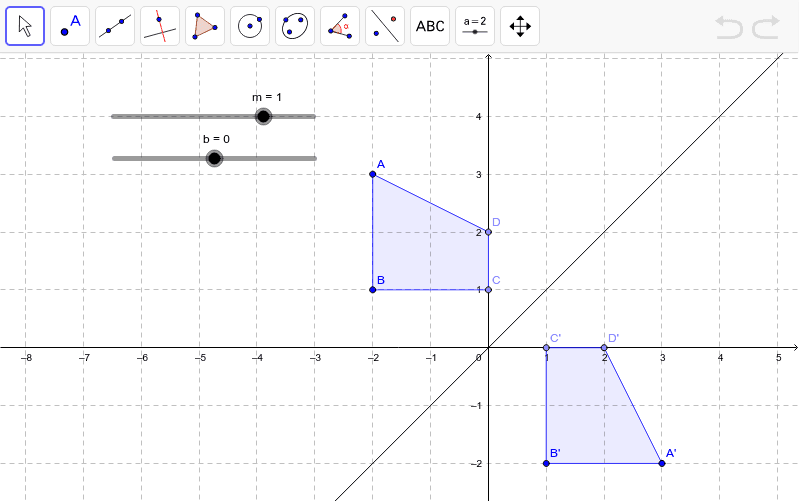



Reflection Over Y Mx B Geogebra



Reflection Over Y Axis Geogebra




How To Reflect A Graph Through The X Axis Y Axis Or Origin



0 件のコメント:
コメントを投稿